Publications
Explore our latest research by browsing pre-prints and accepted papers.
Accepted papers
-
 In International Conference on Artificial Intelligence and Statistics, 2026
In International Conference on Artificial Intelligence and Statistics, 2026 -
 In The Fourteenth International Conference on Learning Representations, 2026
In The Fourteenth International Conference on Learning Representations, 2026 -
 In The Fourteenth International Conference on Learning Representations, 2026
In The Fourteenth International Conference on Learning Representations, 2026 -
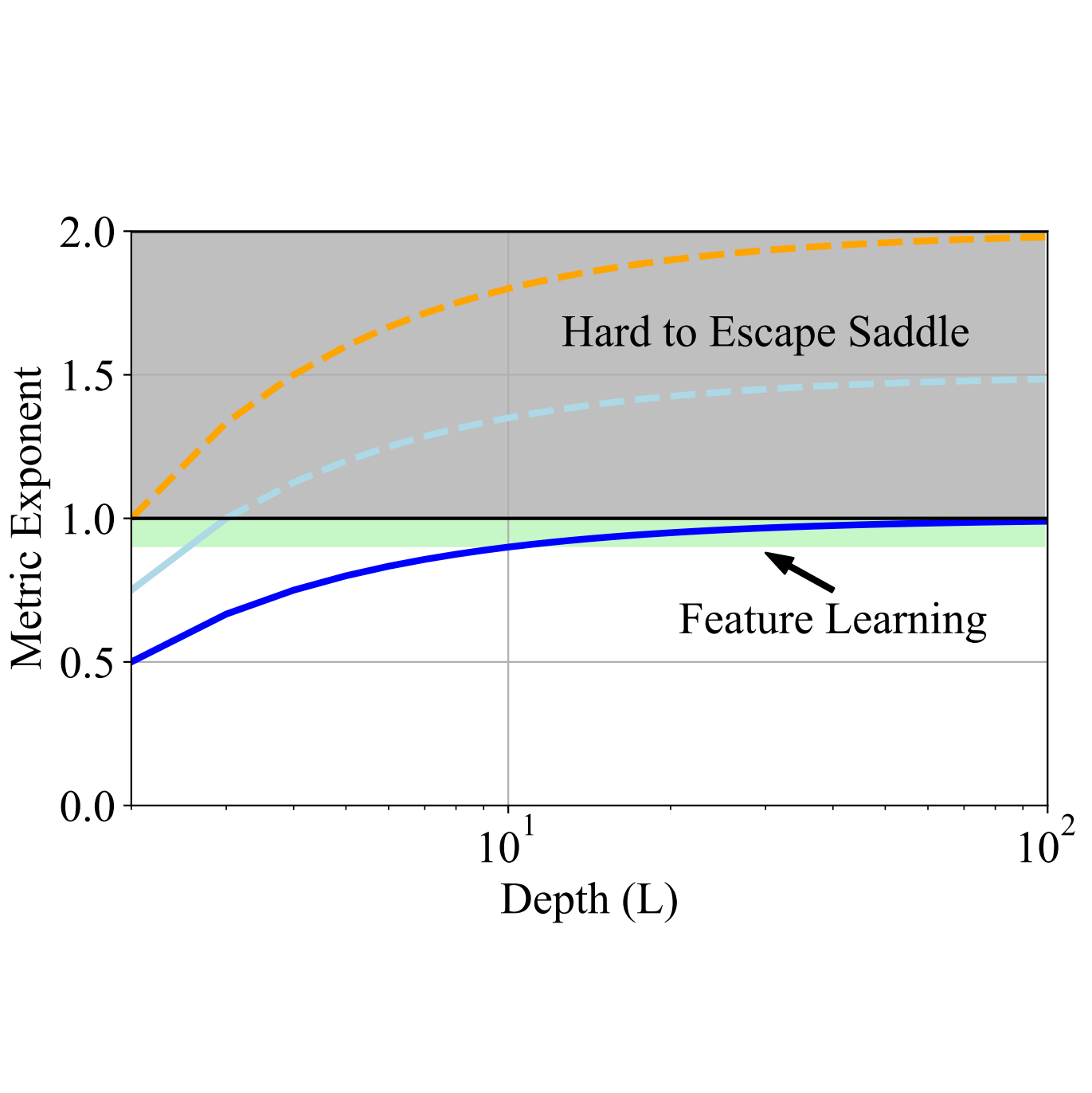 In The Fourteenth International Conference on Learning Representations, 2026
In The Fourteenth International Conference on Learning Representations, 2026 -
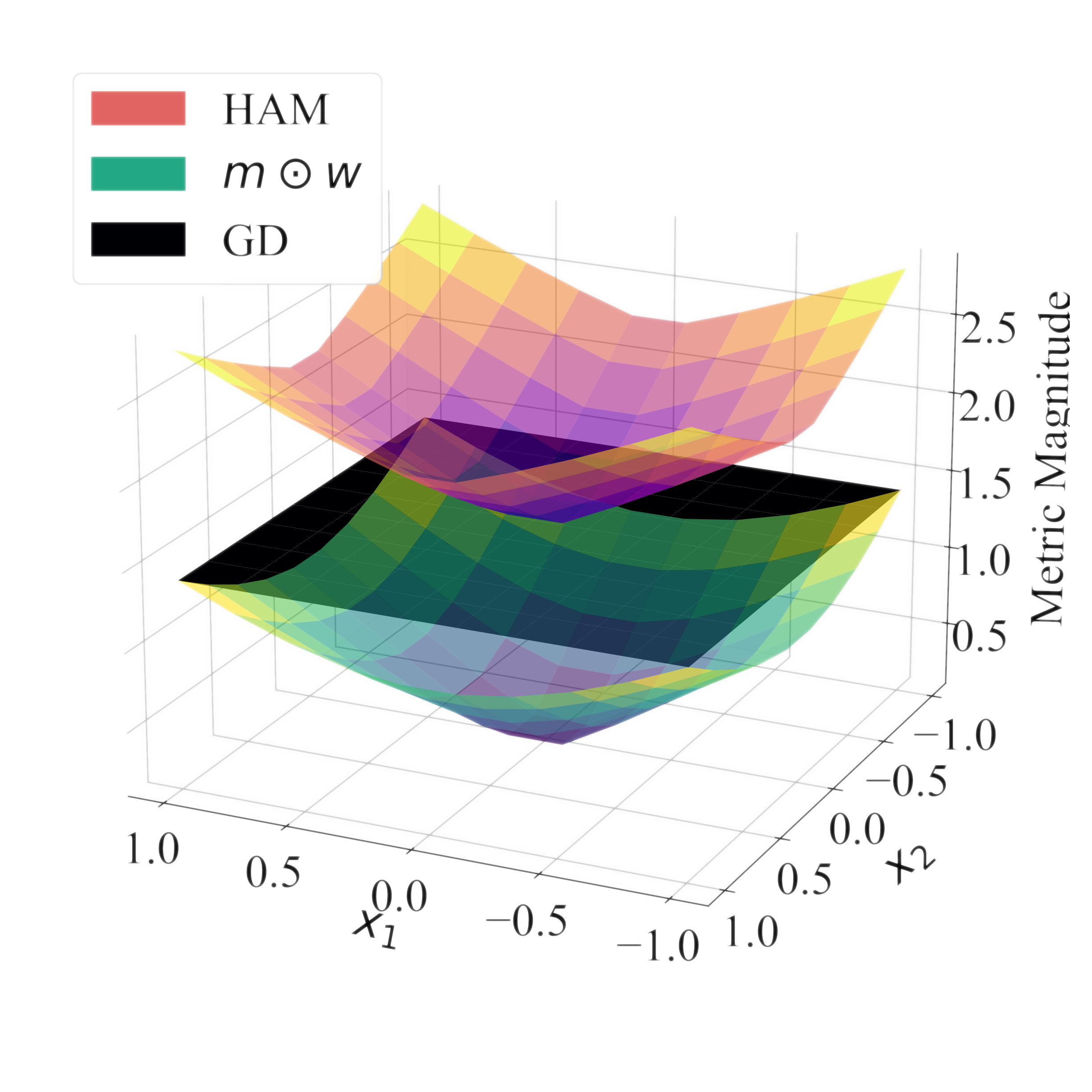 In The Fourteenth International Conference on Learning Representations, 2026
In The Fourteenth International Conference on Learning Representations, 2026 -
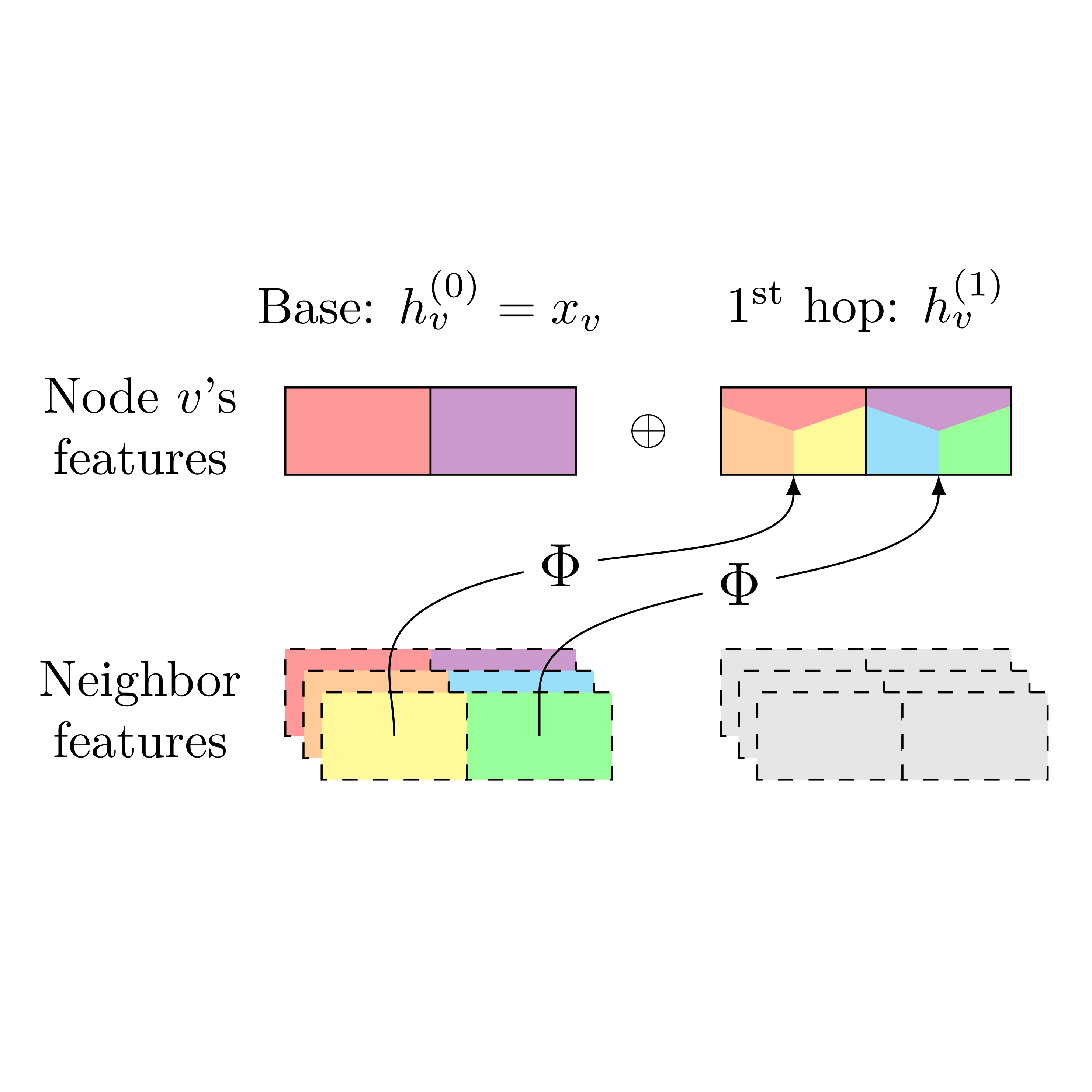 In Women in Machine Learning Workshop @ NeurIPS, 2025
In Women in Machine Learning Workshop @ NeurIPS, 2025 -
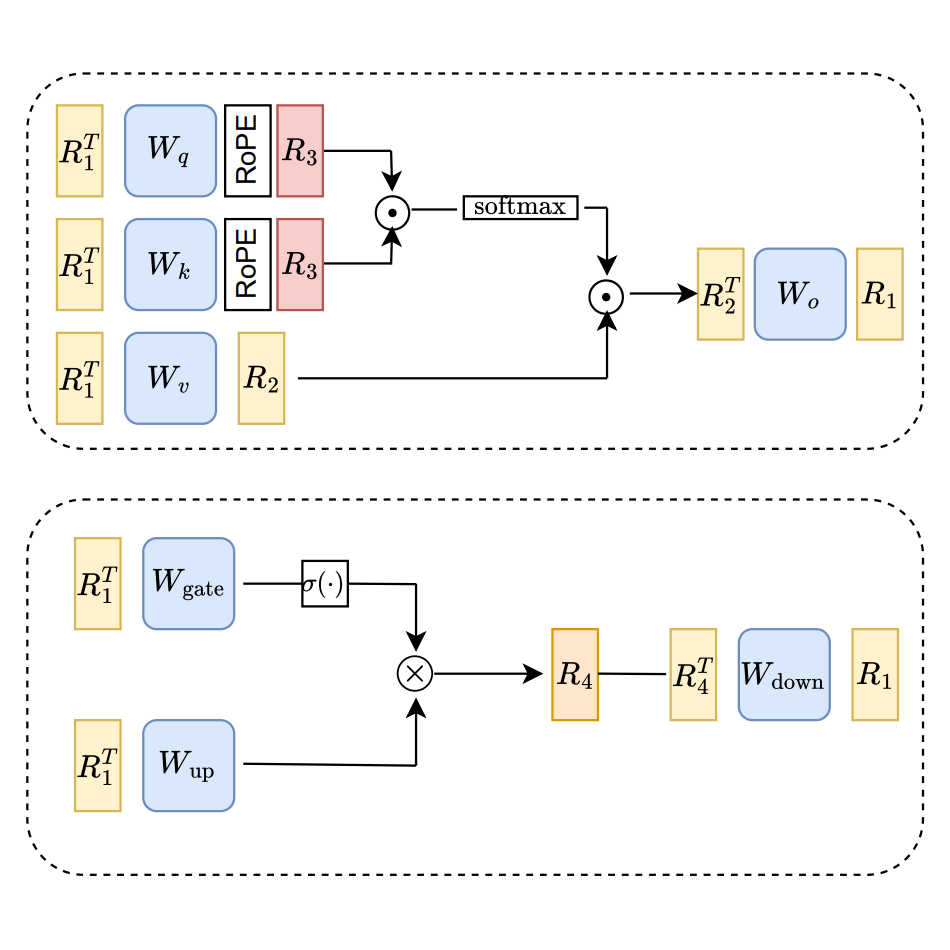 In Machine Learning for Systems @ NeurIPS, 2025
In Machine Learning for Systems @ NeurIPS, 2025 -
 In The Thirty-ninth Annual Conference on Neural Information Processing Systems, 2025
In The Thirty-ninth Annual Conference on Neural Information Processing Systems, 2025 -
 In The Thirty-ninth Annual Conference on Neural Information Processing Systems, 2025
In The Thirty-ninth Annual Conference on Neural Information Processing Systems, 2025 -
 In The Thirty-ninth Annual Conference on Neural Information Processing Systems, 2025
In The Thirty-ninth Annual Conference on Neural Information Processing Systems, 2025 -
 In Forty-second International Conference on Machine Learning, 2025
In Forty-second International Conference on Machine Learning, 2025 -
 In Workshop on Scalable Optimization for Efficient and Adaptive Foundation Models @ ICLR, 2025
In Workshop on Scalable Optimization for Efficient and Adaptive Foundation Models @ ICLR, 2025 -
 In The Thirteenth International Conference on Learning Representations, 2025
In The Thirteenth International Conference on Learning Representations, 2025 -
 In The Thirteenth International Conference on Learning Representations, 2025
In The Thirteenth International Conference on Learning Representations, 2025 -
 In Thirty-eighth Conference on Neural Information Processing Systems, 2024
In Thirty-eighth Conference on Neural Information Processing Systems, 2024 -
 In Thirty-eighth Annual Conference on Neural Information Processing Systems, 2024
In Thirty-eighth Annual Conference on Neural Information Processing Systems, 2024 -
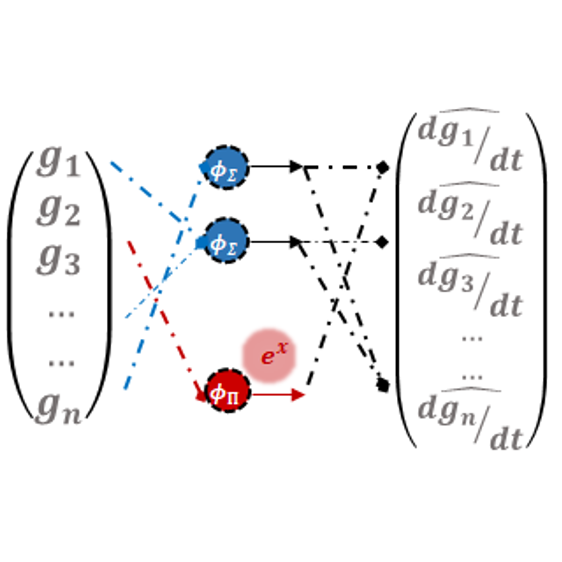 In Thirty-eighth Conference on Neural Information Processing Systems, 2024
In Thirty-eighth Conference on Neural Information Processing Systems, 2024 -
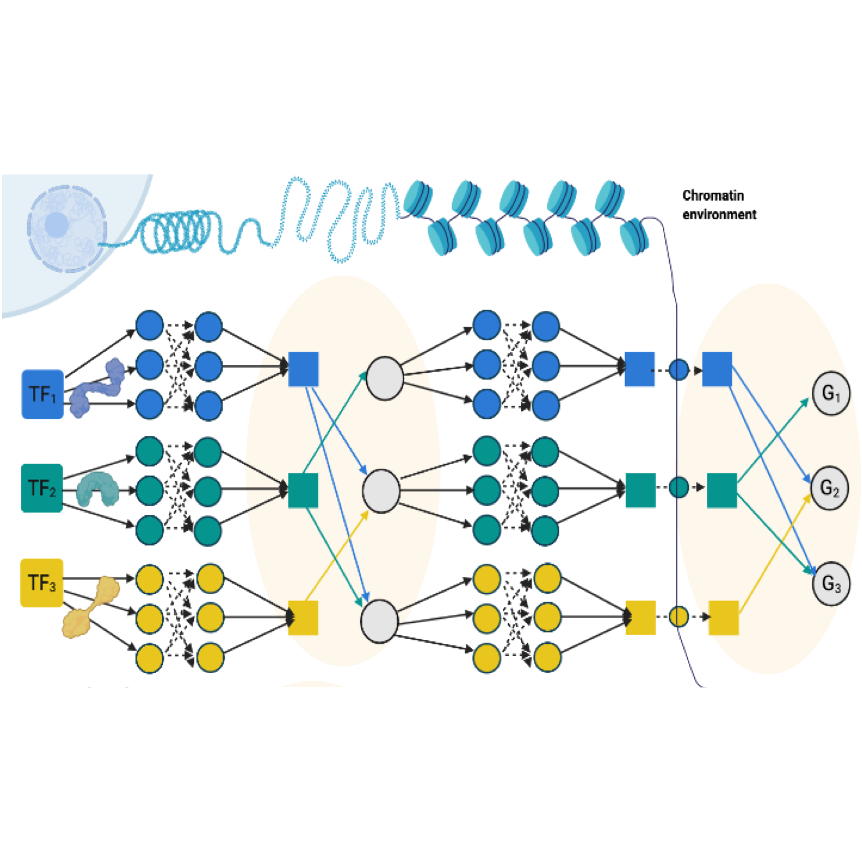 Genome Biology, May 2024
Genome Biology, May 2024 -

-
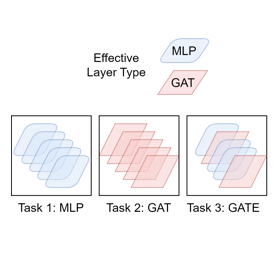 In Forty-first International Conference on Machine Learning, 2024
In Forty-first International Conference on Machine Learning, 2024 -
 In The Twelfth International Conference on Learning Representations, 2024
In The Twelfth International Conference on Learning Representations, 2024 -
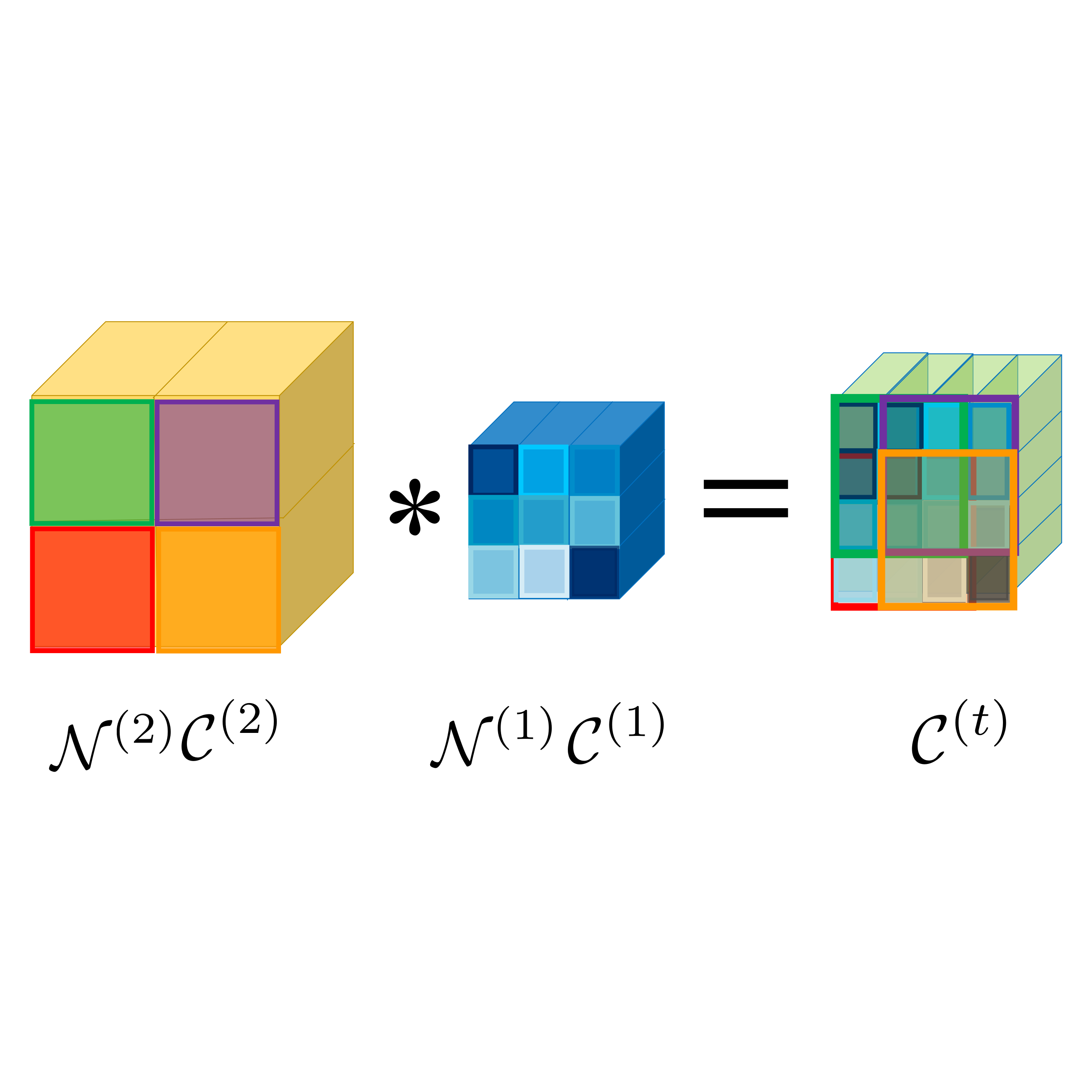 In The Twelfth International Conference on Learning Representations, 2024
In The Twelfth International Conference on Learning Representations, 2024 -
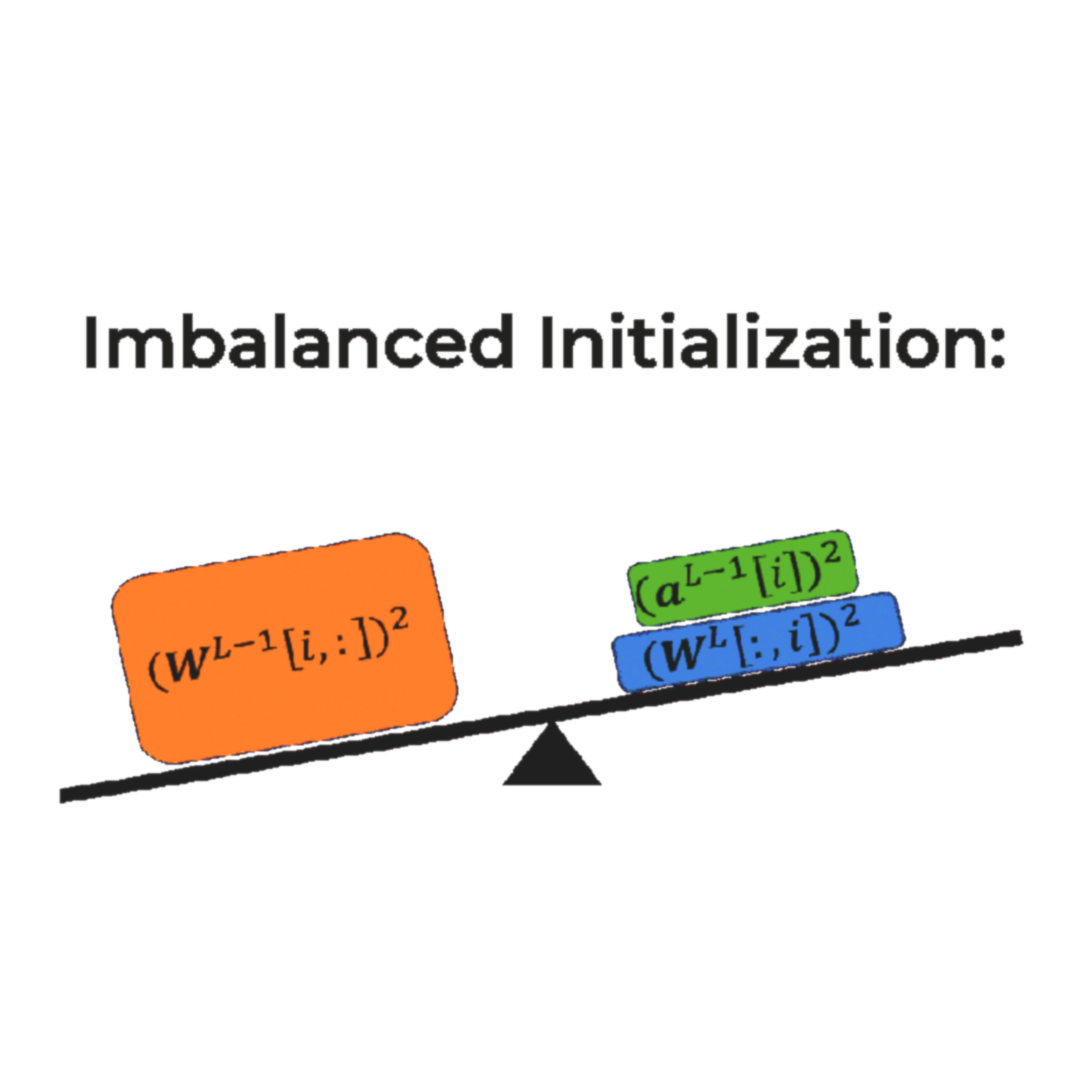 In Thirty-seventh Conference on Neural Information Processing Systems, 2023
In Thirty-seventh Conference on Neural Information Processing Systems, 2023 -
 In Proceedings of the 40th International Conference on Machine Learning, 2023
In Proceedings of the 40th International Conference on Machine Learning, 2023 -
 Nucleic Acids Research, 2022
Nucleic Acids Research, 2022 -
 In Advances in Neural Information Processing Systems, 2022
In Advances in Neural Information Processing Systems, 2022 -
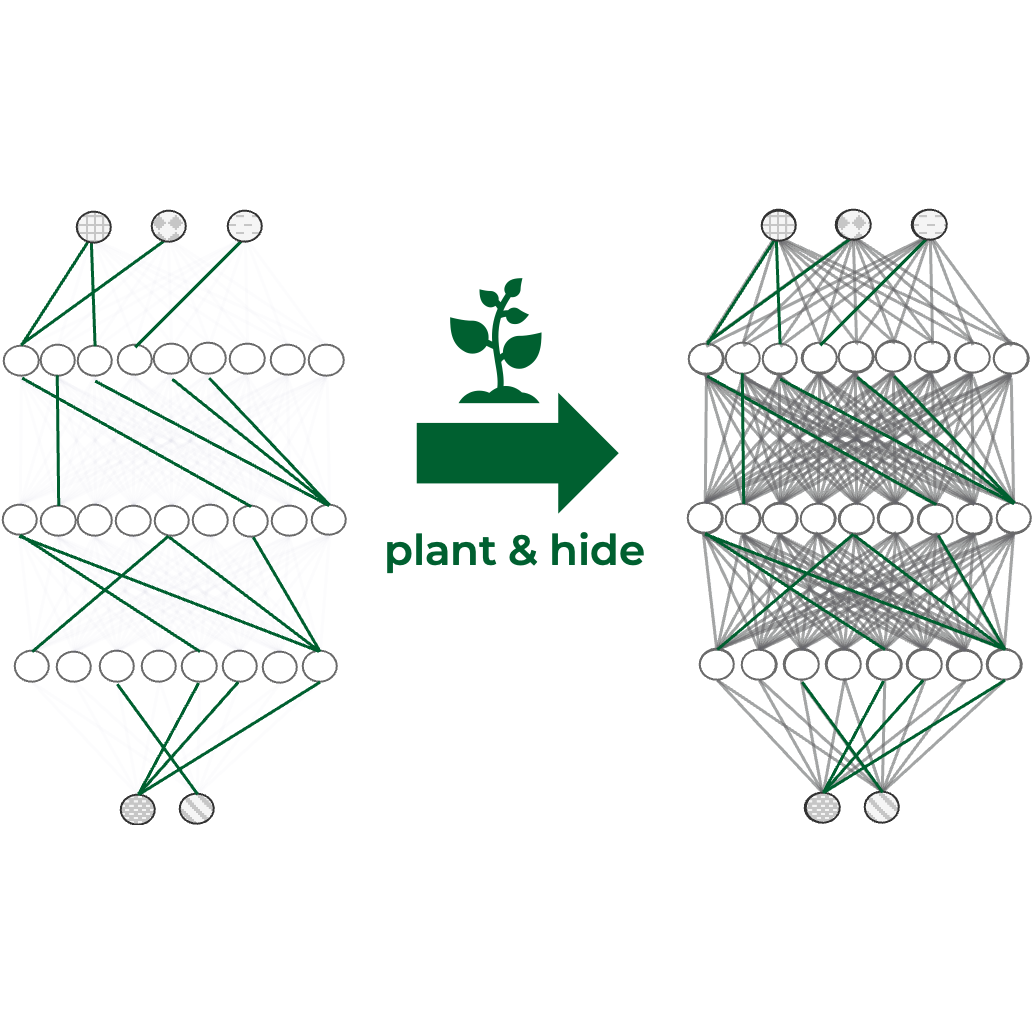 In The Tenth International Conference on Learning Representations, 2022
In The Tenth International Conference on Learning Representations, 2022 -
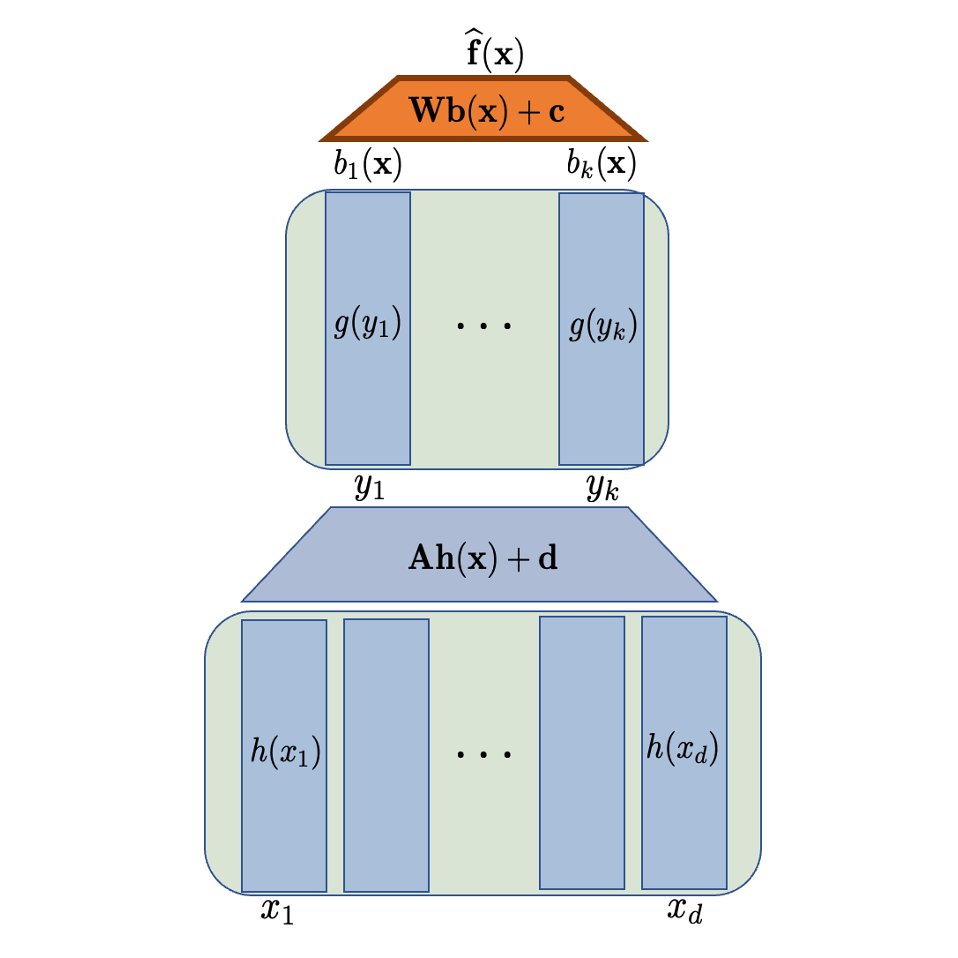 In The Tenth International Conference on Learning Representations, 2022
In The Tenth International Conference on Learning Representations, 2022